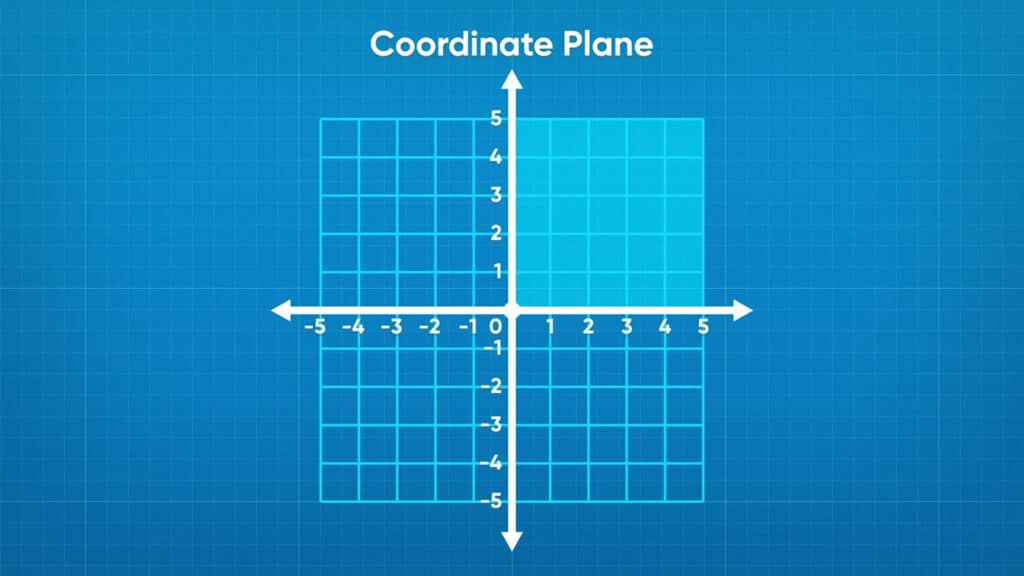
A number line goes on infinitely in both directions; so do the axes on a coordinate grid. Up until now, you only plotted points in the section of the coordinate plane where both x– and y-values were positive. You can also plot points where either value (or both!) is negative.
To better understand using all 4 quadrants of the coordinate plane…
LET’S BREAK IT DOWN!
Expanding the coordinate grid.
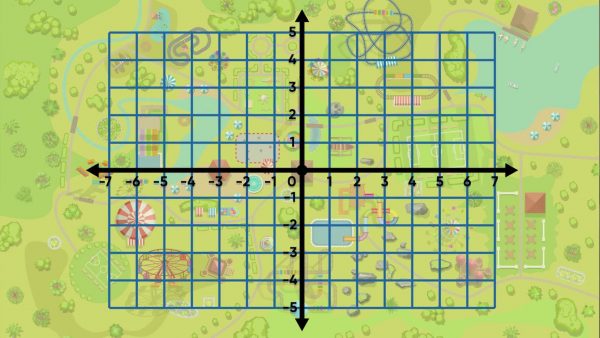
An amusement park uses a coordinate grid to map out locations for rides. The coordinate grid shows new numbers now: the y-axis extends past 0 to the negative numbers, and so does the x-axis. There are now four sections, or quadrants, on the grid. Try this yourself: Identify the quadrant on the coordinate grid where you have plotted points before.
Plot points in all four quadrants in the coordinate grid.
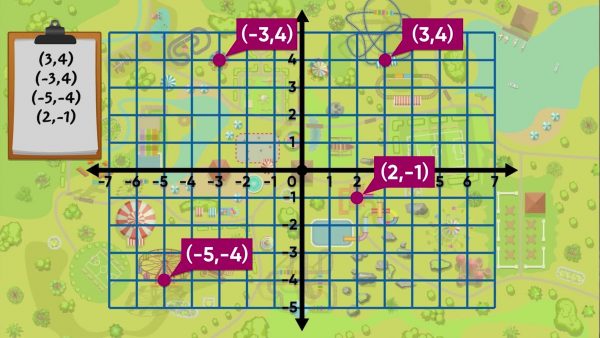
The locations of four rides at the park are: Radical Rollercoaster (3, 4), Elevator Doom Drop (−3, 4), Tilt-A-Whirl (−5, −4), and Raging Rapids Raft Adventure (2, −1). To locate the Radical Rollercoaster, start at the origin and go right 3 units on the x-axis to 3. Then move up 4 to the point (3, 4). To locate the Doom Drop Tower, move 3 units to the left of 0 on the x-axis to −3. Next, move up 4 units from 0 on the y-axis to 4. To locate the Tilt-A-Whirl, move left from 0 on the x-axis 5 units and down 4 units below 0 on the y-axis to the point (−5, −4). To locate Raging Rapids, at point (2, −1), move 2 units to the right of 0 on the x-axis and 1 unit below 0 on the y-axis. Try this yourself: Describe how you would plot the Gift Shop at (−2, −2).
Draw and measure lines on the coordinate grid.
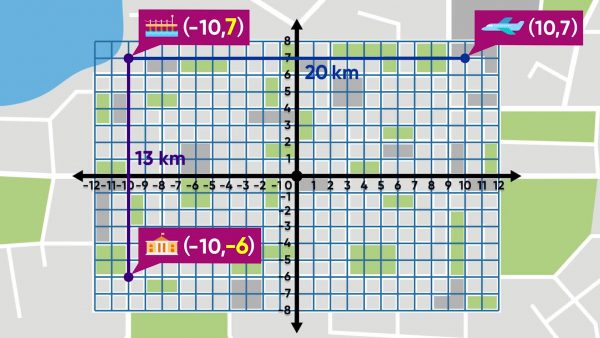
You need to find the distance between two locations on a city map. The pier is at (−10, 7) and the airport is at (10, 7). Both landmarks have the same y-coordinate, so they lie on a horizontal line. The distance is the number of units from one x-coordinate to the other. From −10 to 10 is 20 units. If each unit is 1 kilometer, the distance between these locations is 20 kilometers. You can also subtract the x-coordinates to find the distance: 10--10=20. To find the distance from the pier at point (−10, 7) and City Hall at point (−10, −6), subtract the y-coordinates: 7--6 = 13. The Pier and City Hall are 13 kilometers apart. Try this yourself: What is the distance between the Art Museum at (4, −6) and the Hotel at (4, −2)?
Find the perimeter of a shape using coordinates.
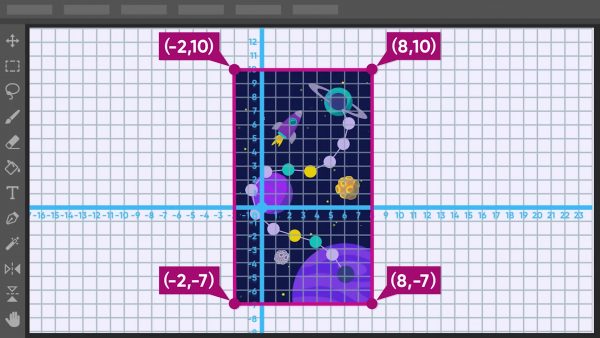
You’ve designed a board game on a coordinate grid on the computer. The gameboard is a rectangle with vertices at (8, 10), (8, −7), (−2, −7), and (−2, 10). You need to calculate the area and perimeter of the gameboard. First, find the side lengths of the rectangle. Find the vertical distance between (8, 10) and (8, −7): 10-(-7) = 17. One side length is 17 units. Next, find the horizontal distance between the points (8, –7) and (–2, –7): 8-(-2) = 10. The other side length is 10 units. On a rectangle, opposite sides have equal length. The perimeter is the sum 17+10+17+10=54 units. If 1 unit is equal to 1 centimeter, the board game has perimeter 54 centimeters. The area of the rectangle is length times width, or 17 × 10=170 square centimeters. Try this yourself: What is the perimeter of a rectangle with vertices at (2, 2), (−2, 2), (−2, −2) and (2, −2)?
USE ALL 4 QUADRANTS OF THE COORDINATE PLANE VOCABULARY
USE ALL 4 QUADRANTS OF THE COORDINATE PLANE DISCUSSION QUESTIONS
Describe how to locate the point (–9, 7) on the coordinate grid.
What are two different ways to find the length of a line segment between points
(–3, 5) and (6, 5)?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More






