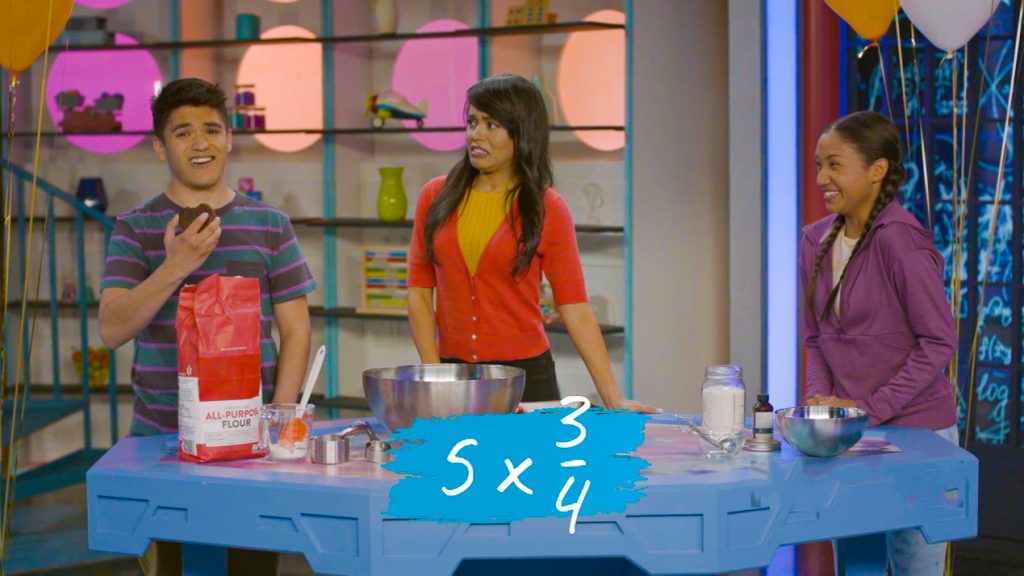
Students connect repeated addition of fractions to multiplying fractions by whole numbers. After exploring examples in many different contexts where a fraction is multiplied by a whole number, they develop the following rule: Multiply the whole number by the fraction’s numerator and keep the fraction’s denominator.
To better understand multiplying fractions by whole numbers…
LET’S BREAK IT DOWN!
Planning a Pizza Party for 8 People

Multiplying fractions by whole numbers can help you determine how many pizzas to order for a pizza party. Let’s say you were having 7 friends over for a pizza party and you want to eat too, how many pies do you need to order if everyone will get one slice? We can figure this out by thinking of a pizza slice as a fraction. Since pizzas are cut into 8 pieces, one pizza slice can be represented by the fraction [ggfrac]1/8[/ggfrac]. Since we need 8 of those fractions, we can represent that as [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] which is equal to [ggfrac]8/8[/ggfrac]. The fraction [ggfrac]8/8[/ggfrac] is the same as the whole number 1. We can also represent that repeated addition as 8 × [ggfrac]1/8[/ggfrac] which is still equal to [ggfrac]8/8[/ggfrac] (one pizza). Remember that multiplication is just repeated addition. Try this one yourself: Let’s say 24 total people will be at the party and each person will get one slice, how many pizzas do you need to order in that case?
Planning a Pizza Party for 32 People

Let’s say you want to have a really big pizza party with 32 guests. How many pizzas do you need to order if everyone will get one slice? Since pizzas are cut into 8 pieces, one pizza slice can be represented by the fraction [ggfrac]1/8[/ggfrac]. For our party, we need 32 of those fractions. We can represent that by writing an expression where [ggfrac]1/8[/ggfrac] is written 32 times. That’s a lot of writing to do. A simpler way to represent it is by using multiplication: 32 × [ggfrac]1/8[/ggfrac]. We would multiply 32 × 1 to get the numerator and keep the denominator 8. 32 × [ggfrac]1/8[/ggfrac] = [ggfrac]32/8[/ggfrac]. Now we probably don’t want to call the pizza place and say we want [ggfrac]32/8[/ggfrac] pizzas. So we need to simplify the fraction [ggfrac]32/8[/ggfrac]. Since 8 four times is 32, [ggfrac]32/8[/ggfrac] is [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac]. And [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] = 1 + 1 + 1 + 1 = 4. So now we know for our 32 guests we need 4 pizzas. Try this one yourself: Let’s say 48 total people will be at the party and each person will get one slice, how many pizzas do you need to order in that case?
Batches of Cookies

Let’s say you have a cookie recipe that calls for [ggfrac]2/3[/ggfrac] cup of flour for one batch of cookies. You decide you want to make four batches of cookies and want to find out how much flour you will need. So you need to find [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. That’s the same as 4 × [ggfrac]2/3[/ggfrac]. We can multiply 4 × 2 to get the numerator of the answer and keep 3 as the denominator. 4 × [ggfrac]2/3[/ggfrac] = [ggfrac]8/3[/ggfrac]. We need [ggfrac]8/3[/ggfrac] of a cup. It will be much easier to work with this number if we simplify it. [ggfrac]8/3[/ggfrac] can be broken down into [ggfrac]3/3[/ggfrac] + [ggfrac]3/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Since [ggfrac]3/3[/ggfrac] equals one, that gives us 1 + 1 + [ggfrac]2/3[/ggfrac] = 2 [ggfrac]2/3[/ggfrac]. You’ll need 2 [ggfrac]2/3[/ggfrac] cups of flour. Try this one yourself: How much flour you’ll need to make 7 small cakes if you need [ggfrac]3/4[/ggfrac] cup flour to make 1 cake.
A Longer Airplane
MULTIPLYING FRACTIONS BY WHOLE NUMBERS VOCABULARY
MULTIPLYING FRACTIONS BY WHOLE NUMBERS DISCUSSION QUESTIONS
How would you write [ggfrac]3/4[/ggfrac]+ [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] as a multiplication problem?
Would adding [ggfrac]2/9[/ggfrac] twenty times be the same as 20 x [ggfrac]2/9[/ggfrac]? Which method would you use to solve the problem? Why?
Gita said 4 x [ggfrac]2/5[/ggfrac] = [ggfrac]8/20[/ggfrac]. Is Gita right? Explain.
Husam says the answer to 6 x [ggfrac]1/3[/ggfrac] is less than 1 because [ggfrac]1/3[/ggfrac] is less than 1. Is Husam right? Explain.
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More






