Read About Multiplying Fractions by Fractions

Birthday Cake Let’s say you have two-thirds of a birthday cake and you want to find out how much will be left if you eat [ggfrac]3/4[/ggfrac] of what is left. You can model this by dividing a rectangle into 3 equal parts with vertical lines. Then color in two of those parts with color 1. Now you can divide the rectangle into fourths using horizontal lines. You can use a different color to color in 3 of those 4 parts to represent [ggfrac]3/4[/ggfrac]. The part that remains colored by color 1 but not color 2 is the amount of cake that will be left after you eat [ggfrac]3/4[/ggfrac] of [ggfrac]2/3[/ggfrac] of a birthday cake. The remaining section is [ggfrac]2/12[/ggfrac] or [ggfrac]1/6[/ggfrac] of the whole cake. Try this one yourself. You have [ggfrac]4/5[/ggfrac] of a birthday cake left. You eat [ggfrac]1/3[/ggfrac] of what is left. How much of the whole cake is left now?

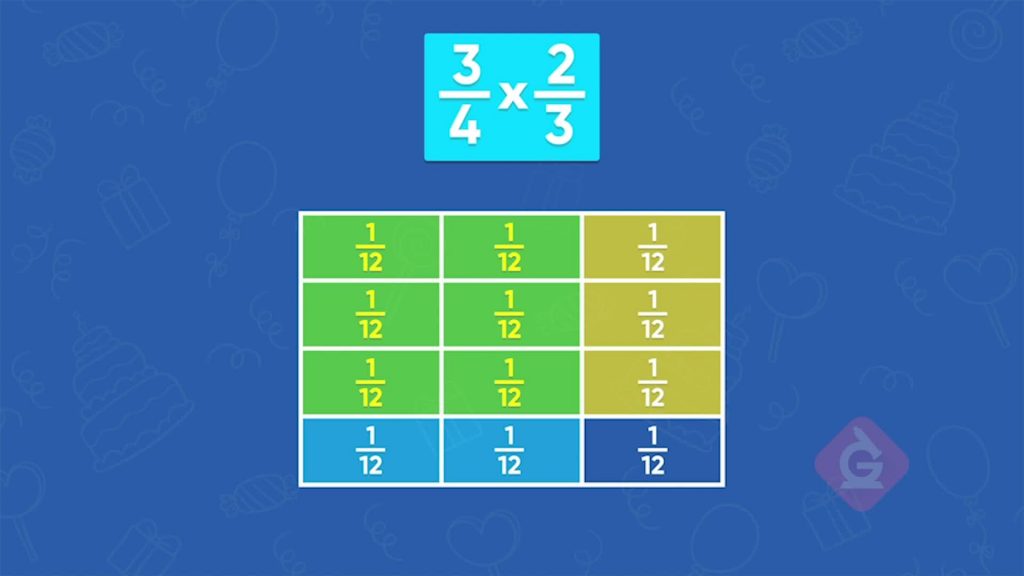
Mac N Cheese Let’s say you have a recipe for macaroni and cheese that calls for [ggfrac]5/6[/ggfrac] of a pound of cheese. You know that [ggfrac]3/5[/ggfrac] of the cheese must be cheddar cheese. You want to find out how many pounds of cheddar cheese you need. Find [ggfrac]3/5[/ggfrac] of [ggfrac]5/6[/ggfrac] by multiplying [ggfrac]3/5[/ggfrac] times [ggfrac]5/6[/ggfrac]. Take a square and divide it vertically into 6 equal sections. Shade 5 out of the 6 sections blue. Now split the square horizontally into 5 equal sections and highlight 3 of the sections yellow. The overlapping sections in green represent the product. Each part of the square is [ggfrac]1/30[/ggfrac] of the square and 15 of those parts are shaded green. You need [ggfrac]15/30[/ggfrac] or [ggfrac]1/2[/ggfrac] pound of cheddar cheese. You can also get that answer by multiplying the denominators. [ggfrac]5/6[/ggfrac] x [ggfrac]3/5[/ggfrac] = [ggfrac]15/30[/ggfrac] = [ggfrac]1/2[/ggfrac]. Try this one yourself. Another recipe calls for [ggfrac]1/2[/ggfrac] pound of cheese and [ggfrac]3/8[/ggfrac] of that must be cheddar cheese. How much cheddar cheese do you need?

Puppets Let’s say the instructions to make a puppet say you need a piece of felt that is [ggfrac]1/4[/ggfrac] yard long. However, your teacher asks you to use a piece that is 2[ggfrac]2/3[/ggfrac] times longer, to make a bigger puppet. To find the length of felt that you need, find the product of 2[ggfrac]2/3[/ggfrac] x [ggfrac]1/4[/ggfrac]. First, convert 2[ggfrac]2/3[/ggfrac] into a fraction greater than 1: [ggfrac]8/3[/ggfrac]. Next, find [ggfrac]8/3[/ggfrac] x [ggfrac]1/4[/ggfrac] by multiplying the numerators and then the denominators:[ggfrac]8/3[/ggfrac] x [ggfrac]1/4[/ggfrac] = [ggfrac]8x1/3x4[/ggfrac] = [ggfrac]8/12[/ggfrac]. The piece of felt should be [ggfrac]8/12[/ggfrac] yard long. Try this one yourself. You need a piece of felt that is 1[ggfrac]3/4[/ggfrac] times longer than [ggfrac]1/8[/ggfrac] yard. What is the length of the piece of felt you need?

Track Team Let's say you run 1[ggfrac]1/3[/ggfrac] miles every day. Your coach tells you that you need to run 2[ggfrac]1/4[/ggfrac] times that distance. You want to find out how far you need to run each day now. You need to find 1[ggfrac]1/3[/ggfrac] x 2[ggfrac]1/4[/ggfrac]. First, convert both mixed numbers to fractions greater than 1: 1[ggfrac]1/3[/ggfrac] = [ggfrac]4/3[/ggfrac] and 2[ggfrac]1/4[/ggfrac] = [ggfrac]9/4[/ggfrac]. Now you can find the product: [ggfrac]4/3[/ggfrac] x [ggfrac]9/4[/ggfrac] = [ggfrac]36/12[/ggfrac] = 3. You need to run 3 miles each day. Try this one yourself. Your friend runs 1[ggfrac]1/2[/ggfrac] miles each day but his coach tells him he needs to run 1[ggfrac]3/4[/ggfrac] times that distance. What distance does your friend need to run?