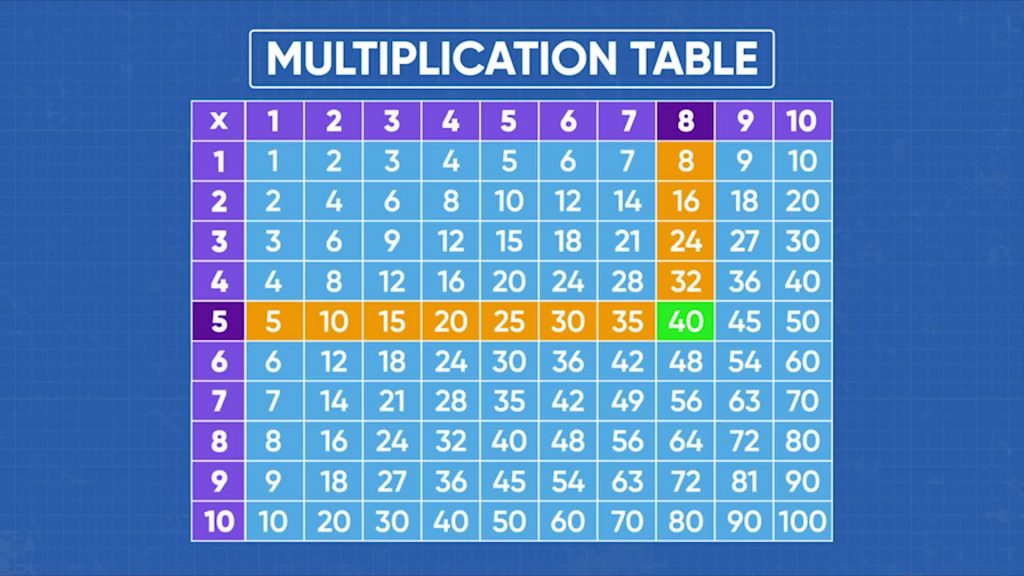
Multiplication is a shorter way to write and calculate repeated addition. A multiplication table can help you find answers to multiplication problems.
To better understand intro to multiplication…
LET’S BREAK IT DOWN!
Six-Packs of Bottles
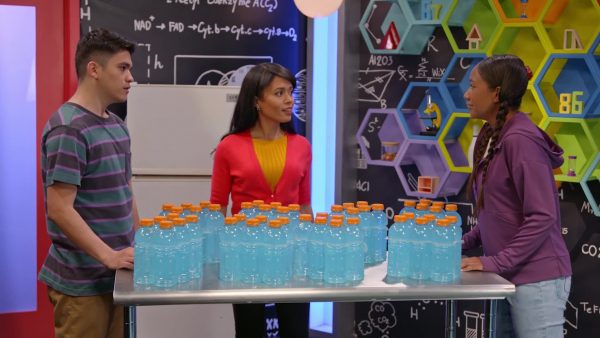
Let’s say you have 8 six-packs of soda bottles. How many soda bottles do you have in all? We could count all of the bottles one at a time but it’s easier to count in groups of 6. So we start with 6 and add 8 sixes. 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6. Since each group has 6 bottles in it, we can also show this in what is called an array by making 8 rows with 6 bottles in each row. We can count the rows by 6. 6, 12, 18, 24, 30, 36, 42, 48. There are 48 soda bottles. Since we have 8 groups of 6, we can say 8 times 6 is equal to 48 (8 x 6 = 48). That’s multiplication and we can write 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 8 x 6 = 48. Multiplication is a faster way to do repeated addition. Try this one yourself. If you have 4 six-packs of soda bottles, how many soda bottles do you have in all?
8-Wheel Trucks

Let’s say there are 5 trucks with 8 wheels each and we want to replace all of their wheels. How many total wheels is that? Each truck has a group of 8 wheels so we can make an array with equal groups of 8. The array has 5 rows with 8 wheels in each row. This array represents the multiplication expression 5 x 8. When we count by eights – 8, 16, 24, 32, 40 – we see there are 40 wheels in all. We can write the multiplication equation 5 x 8 = 40. 5 and 8 are called factors and 40 is called the product. Try this one yourself. How many total wheels are on 7 trucks with 8 wheels each
Basketball

Let’s say you want to keep track of multiplication problems that you use often. You can make a multiplication table to keep track of answers to multiplication problems. Each row in the table represents counting by equal groups of different sizes. One way you can use the table is to keep track of scores in basketball. One kind of shot in a basketball game is called a field goal and you get 3 points for it. You can use the table to see how many points you will get in all for different numbers of 3-point shots. Look at the row that starts with 3. The row with 3 has the following numbers in it: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. Along the top of the table it shows how many times the number 3 has been multiplied. If there were five 3-point shots I would want to know what 5 x 3 is. I can see where 5 and 3 intersect in the table to find the product. 5 and 3 intersect at 15 so 5 x 3 = 15. Try this one yourself. What numbers would be in the row that starts with 6 in the multiplication chart? How could you use the multiplication chart to find the answer to 6 x 4?
Cupcakes
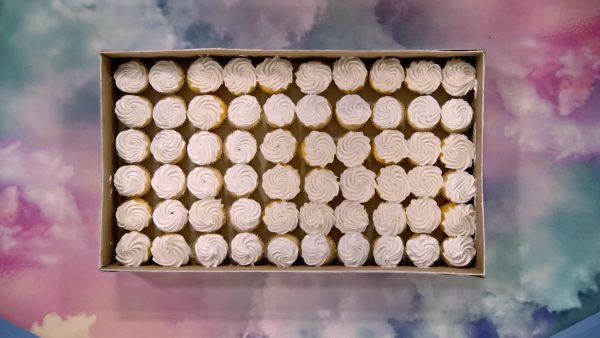
Let’s say you have an array of 6 rows of cupcakes with 10 cupcakes in each row. How many cupcakes are there in all? To find out we need to find the product of 6 x 10. We can use the multiplication table to see that 6 and 10 intersect at 60. So we have 60 cupcakes in all. We can also see that 10 and 6 also intersect at 60. We can look at arrays to see why this is true. We can show 6 x 10 with an array with 6 rows and 10 in each row. We can show 10 x 6 with an array with 10 rows and 6 in each row. Both of these arrays have 60 in them. And if we turn one of the arrays we can see that it exactly fits on top of the other array. Try this one yourself. Use a multiplication table and arrays to show that 5 x 3 has the same product as 3 x 5.
INTRO TO MULITPLICATION VOCABULARY
INTRO TO MULITPLICATION DISCUSSION QUESTIONS
How can you model 8 + 8 + 8 + 8 and write it as a multiplication equation?
O O O O O O O O
O O O O O O O O
O O O O O O O O
O O O O O O O O
4 x 8 = 32
Create a word problem where the expression 7 x 6 could be used to find the answer.
Amin said that the expression 4 x 3 has a value of 7. Is he correct? If not, what did he do wrong?
Which addition expression could be easily changed to a multiplication expression with the same value, 4 + 3 + 4 + 3 + 2 or 4 + 4 + 4 + 4 + 4? Explain
If you multiply 7 x 5, will you get the same answer as if you multiply 5 x 7? Explain.
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More






