
Algebraic equations can have 1 solution. They may also have infinitely many solutions, which means that any value of the variable makes the equation true. They may also have no solutions, which means that no value of the variable makes the equation true.
To better understand how to determine the number of solutions for linear equations …
LET’S BREAK IT DOWN!
Review how to solve an equation.
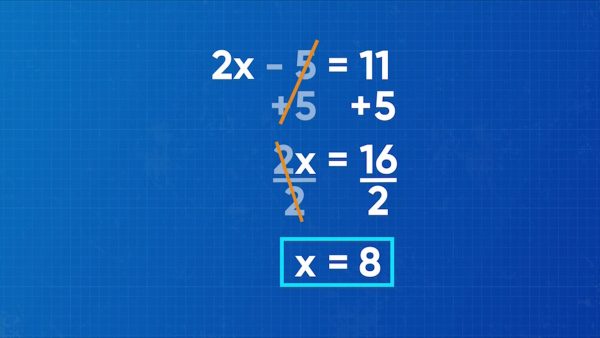
Emily wants to solve the equation 2x-5=11. She knows she needs to do two steps to solve and use inverse operations to isolate the x. First, 5 is subtracted on the left side, so add 5 to both sides of the equation. 2x-5+5=11+5. This simplifies to 2x=16. Next, the x is multiplied by 2, so divide both sides by 2. [ggfrac]2x/2[/ggfrac] = [ggfrac]16/2[/ggfrac]. This simplifies to x=8. x has been isolated, so you know that x is equal to 8. Try this yourself: Solve for x in the equation 3x+5=17.
Equations can have one solution.
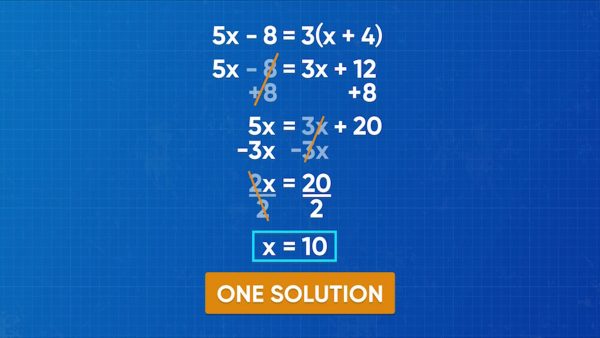
Emily wants to solve the equation 5x-8=3(x+4). This equation takes multiple steps to solve and has variables on both sides of the equation! On the right side, the 3 is multiplied by an expression in brackets. To simplify the right side, you need to use the distributive property. Multiply 3 by every term inside the brackets. 3(x + 4) = 3(x) + 3(4) = 3x + 12. Now the equation can be written as 5x-8=3x+12. Isolate the x-terms on one side of the equation (it doesn’t matter which side). Emily decides to put the x-terms on the left side, so she focuses on eliminating the -8 first. Add 8 to both sides. 5x-8+8=3x+12+8, which simplifies to 5x=3x+20. Next, subtract 3x from both sides. 5x-3x=3x+20-3x, which simplifies to 2x=20. The last step to isolate the x is to divide both sides by 2. [ggfrac]2x/2[/ggfrac] = [ggfrac]20/2[/ggfrac]. Then x = 10. The equation has one solution, and that solution is 10. Try this yourself: Solve for x in 8x-12=-4(x+6).
Equations can have no solutions.

Adesina is solving 4x+8=4x+10. There is a variable on both sides of the equal sign, so move the variables to one side and the constants to the other. It doesn’t matter which you do first. First, let's remove the + 8 from the left side by subtracting 8 from both sides. 4x+8-8=4x+10-8, which simplifies to 4x=4x+2. Next, remove the 4x from the right side by subtracting 4x from both sides. 4x-4x=4x+2-4x, or 0=2. This equation is not true! It does not matter what value of x you choose, you cannot make the left and right sides of the equation equal. This means that the equation has no solutions. Try this yourself: Show algebraically that 2x+4=2x+8 has no solutions.
Equations can have infinitely many solutions.

Emily is solving 12+3x=3x+12. Let's start by removing the 12 from the left side. So, subtract 12 from both sides: 12+3x-12=3x+12-12. When simplified this becomes 3x=3x. Next, remove the 3x from the right side by subtracting 3x from both sides. 3x-3x=3x-3x, which simplifies to 0=0. This statement is true. It doesn’t matter what value of x you choose, the left side is equal to the right side. This means that there are infinitely many solutions. Try this yourself: Show algebraically that 4+10x=2(5x+2) has infinitely many solutions.
DETERMINING THE NUMBER OF SOLUTIONS FOR LINEAR EQUATIONS VOCABULARY
DETERMINING THE NUMBER OF SOLUTIONS FOR LINEAR EQUATIONS DISCUSSION QUESTIONS
What is the distributive property?
When you solve an equation until there are no variables left, what are the possible solutions to the problem?
How can you tell if an equation has infinitely many solutions?
How can you tell if an equation has no solutions?
How can you tell if an equation has one solution?
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More






