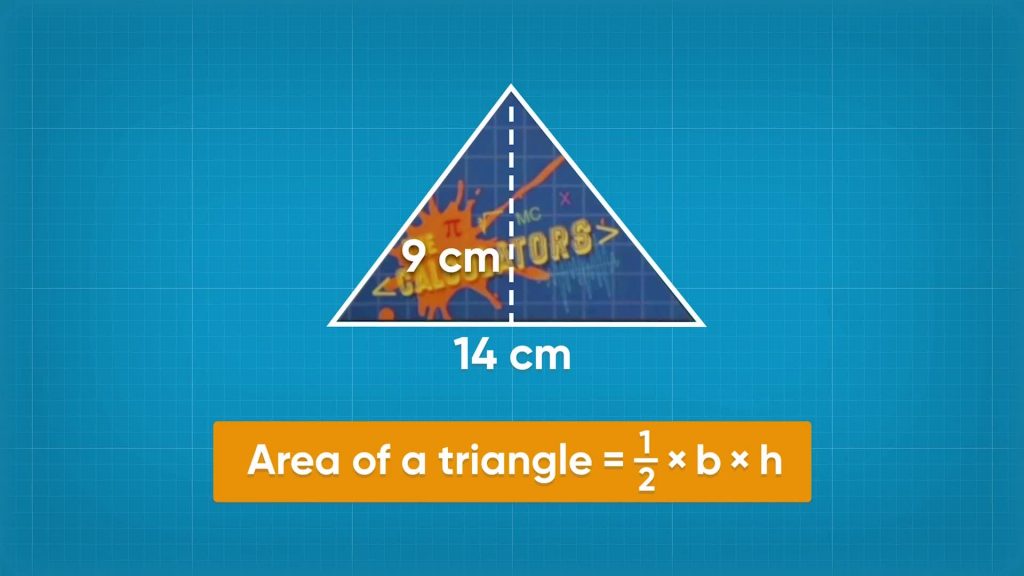
A formula is a rule written with mathematical symbols that connects two or more quantities with an equal sign. Formulas for area tell you the area of a shape given certain dimensions.
To better understand Area of Triangles & Quadrilaterals (using formulas)…
LET’S BREAK IT DOWN!
Armadillo Pen

Let’s say you want to make a pen in the shape of a parallelogram for an armadillo. A parallelogram has 4 sides and the opposite sides are parallel. To find out how much sand you need to cover the floor, you need to find the area of the parallelogram. To help find the area, you can decompose the parallelogram into a rectangle and two triangles. You know how to find the area of a rectangle and you can move these parts around to make a rectangle. Then you can use the formula for the area of a rectangle, which is A = bh. The parallelogram has base 7 m and height 4 m. 7 × 4 = 28. So the area of the parallelogram is 28 square meters. Try this one yourself. For another animal you want to make a pen in the shape of a parallelogram that has base 9 m and height 6 m. What is the area of the pen?
Band Stickers

Let’s say you want to make stickers for your band in the shape of a triangle. You need to know the area of the stickers to find out the cost. You can use what you learned about parallelograms to find to find the area of a triangle. You cut the parallelogram in half to get two triangles that are each exactly half of the parallelogram. Since the area of a parallelogram is base times height, the area of one triangle is [ggfrac]1/2[/ggfrac]bh. One of the triangles has base 12 cm and height 5 cm. [ggfrac]1/2[/ggfrac]×12=6, and 6 × 5 = 30. So the area of this sticker is 30 square centimeters. Try this one yourself. You have another triangular sticker that has base 8 cm and height 5 cm. What is the area of this sticker?
Refurbishing a Desk
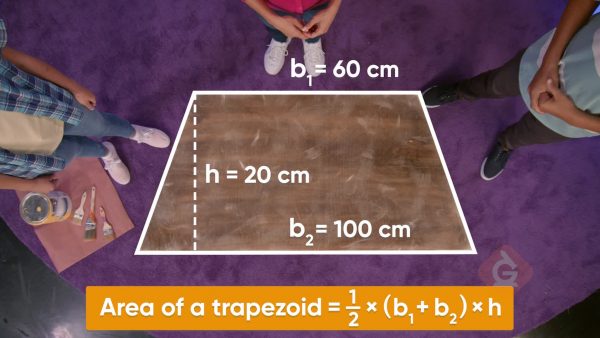
Let’s say you want to paint a desktop that is in the shape of a trapezoid. You need to find the area of the trapezoid to make sure you have enough paint. You decide to call the top side b1 and the bottom side b2. The vertical measurement is the height. You can make a copy of the trapezoid, rotate it 180 degrees, and join it with the first trapezoid. Now you have a parallelogram. The area of the trapezoid is half the area of the parallelogram, and you know how to find the area of a parallelogram. The base of the parallelogram is b1 + b2 and the height is h. The formula for the area of the parallelogram is (b1 + b2)h. That means the formula for the area of each trapezoid is [ggfrac]1/2[/ggfrac](b1+b2)h. One of the bases is 120 cm and the other base is 80 cm. The height is 60 cm. Using the formula for area, you get [ggfrac]1/2[/ggfrac](120+80)60, or 6,000 sq cm. Try this one yourself.Another desktop in the shape of a trapezoid has different dimensions. One base measures 100 cm and the other base measures 90 cm. The height is 70 cm. Find the area of this desktop.
Campsites
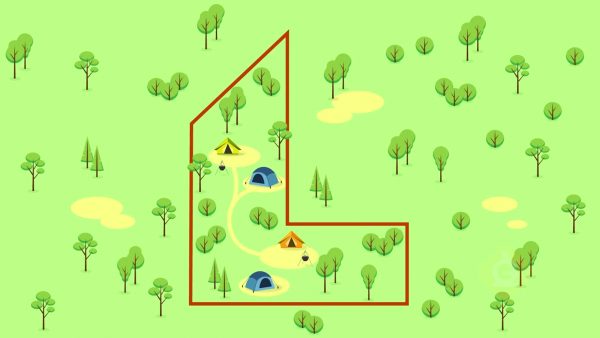
Let’s say you are going on a camping trip with a lot of people and want to make sure that the area of the campsite has enough space for everyone. You look at the map of the campsite and it looks like it has a unique shape. You don’t know how you can compute the area of the site. Then you realize that the shape of the campsite is made up of a trapezoid and a parallelogram. You can find the area of each shape and then add the areas together. You decide to calculate the trapezoid first. One of its bases is 3 m and the other base is 7 m. The height is 2 m. The area of the trapezoid is [ggfrac]1/2[/ggfrac](3+7)2, or 10 sq. m. The base of the parallelogram is 7 m and the height is 3 m. You multiply 7 × 3 to find that its area is 21 sq. m. You add the areas of the two figures. 10 sq. m + 21 sq. m = 31 sq. m. Try this one yourself. You are making a piece of art on a board that has an irregular shape that can be decomposed into a triangle and a parallelogram. You want to find the area of the board. The triangle has base 10 cm and height 15 cm. The parallelogram has base 10 cm and height 8 cm. What is the area of the board?
AREA OF TRIANGLES & QUADRILATERALS (USING FORMULAS) VOCABULARY
AREA OF TRIANGLES & QUADRILATERALS (USING FORMULAS) DISCUSSION QUESTIONS
A triangle has base length 18 inches and height 6 inches. What formula can help you find the area of this triangle? Find the area.
A parallelogram has base 6 m and height 2.5 m. What formula helps you find the area of this parallelogram? Find the area.
A trapezoid has top length 8 cm, bottom length 13 cm, and height 7 cm. What formula can you use to find the area of this trapezoid? Find the area.
How do the formulas you found today relate to the formulas for the area of right triangles and rectangles?
Jasmine has a parallelogram with base length 6 units, side length 4.5 units, and height 4 units. Jasmine says that the area of this parallelogram is 27 square units. Is she correct? Explain.
Skip, I will use a 3 day free trial
Enjoy your free 30 days trial
We use cookies to make your experience with this site better. By using this site you agree to our use of cookies. Click "Decline" to delete and block any non-essential cookies for this site on this specific property, device, and browser. Please read our privacy policy for more information on the cookies we use.Learn More
We use cookies to improve your experience. By using this site, you agree to our use of cookies. Click "Decline" to block non-essential cookies. See our privacy policy for details.Learn More






