Read About Area Of Polygons

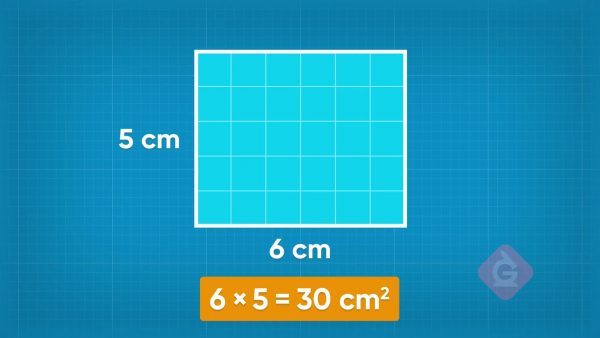
Review the area of a rectangle. Area is the space inside a 2D shape. We measure area in square units. You know that the area of a rectangle is its length multiplied by its width. For example, a rectangle that is 6 cm wide and 5 cm long has area 5 × 6 = 30 square centimeters. You can use the area of a rectangle to find the area of other polygons.

Find the area of a triangle on a skateboard ramp. The side of a skateboard ramp is in the shape of a right triangle. A right triangle has one angle that is 90 degrees. You can make a right triangle by taking a rectangle and dividing it along the diagonal. One rectangle makes 2 right triangles with equal area. A 10 cm by 5 cm rectangle has area 50 cm2. Divide the rectangle along to diagonal to make 2 right triangles that have base and height 10 cm and 5 cm. The area is half of 50, or 25 cm2. The area of a triangle is [ggfrac]1/2[/ggfrac] × base × height. The triangle of the skateboard ramp has base 100 cm and height 30 cm. The area is [ggfrac]1/2[/ggfrac]×100×30 = 1,500 cm2.

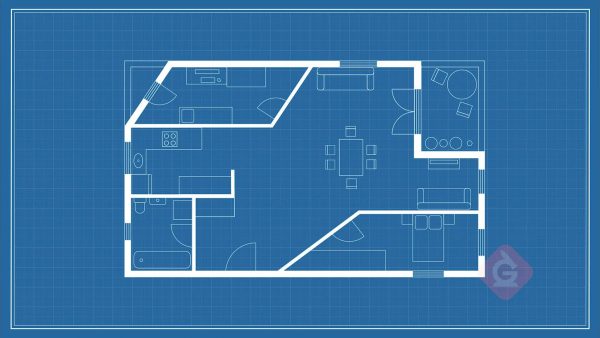
Find the area of polygons in blueprints. A blueprint is a 2D plan that shows the walls of a building. A blueprint you have has a room in the shape of a trapezoid and a room in the shape of a parallelogram. You need to find the area of these rooms to estimate how much flooring to buy. You can decompose polygons into triangles and rectangles to find their area. The trapezoid shape can be divided into one rectangle and one right triangle. The rectangle is 6 meters by 3 meters, so the area is 6 × 3 = 18 m2. The triangle has base 4 meters and height 3 meters, so the area is [ggfrac]1/2[/ggfrac]×4×3 = 6 m2. The total area is 18 + 6 = 24 m2. The parallelogram can be divided into one rectangle and two right triangles. The rectangle has area 5 × 3 = 15 m2. Each triangle has area [ggfrac]1/2[/ggfrac]×3×2 = 3 m2. So, the total area is 15 + 3 + 3 = 21 m2.

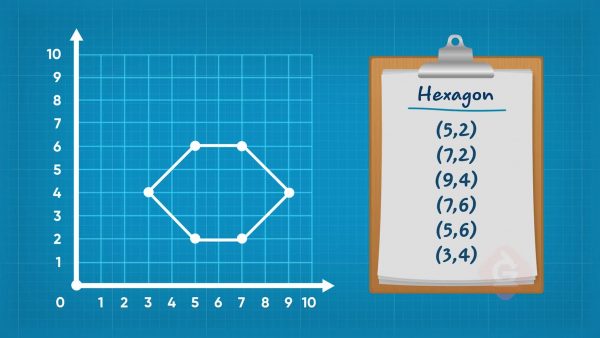
Draw polygons on a coordinate plane. You can plot points on a coordinate plane. A coordinate plane has two axes: the x-axis and the y-axis. A coordinate pair tells you where to plot a point on each axis. The point (8, 5) has x-coordinate 8 and y-coordinate 5. So, you should plot the point 8 units right on the x-axis and 5 units up the y-axis. You can plot points to help you design a video game. To draw a hexagon, you need to plot each point of the shape. To plot the point (5, 2), for example, go right on the x-axis 5 units then go up 2 units. After plotting all of the points, you can draw lines to connect the dots and make the shape.

Find the area of shapes on a coordinate plane. You can find the area of shapes you plot on a coordinate plane. You have a hexagon plotted on the coordinate plane. It has 6 straight sides, and you can divide this hexagon into one rectangle and four right triangles. The area of the rectangle is 5 × 2 = 8 square units. All four triangles have the same area: [ggfrac]1/2[/ggfrac]×2×2 = 2. The total area is 8 + 2 + 2 + 2 + 2 = 16 square units.

There are many careers that use area. Wildlife ecologists are scientists who study animals and how they interact in the wild. It is important to know how much area animals have, to ensure they have what they need. Aerospace engineers calculate the area of designs they make, like the shapes needed to build an airplane. Mural artists use area to plan how to construct their paintings.